大数据时代下的隐私保护（三）

2018-08-02 17:25:3911466人阅读

1.引言

在大数据时代，数据带来了巨大价值的同时,也带来了用户隐私保护方面的难题，如何在大数据开发应用的过程中保护用户隐私和防止敏感信息泄露成为新的挑战。

我们的大数据隐私保护系列文章的第一篇[1]和第二篇[2]主要讲解了k-anonymity(k-匿名化),l-diversity(l-多样化),t-closeness和ε-differential privacy(差分隐私)等四种隐私保护技术的原理和行业应用案例。在用户隐私保护的实践中，数据脱敏是一种常见的技术手段。本文将介绍FPE（Format Preserving Encryption，格式保留加密）技术[3]和基于FPE的数据脱敏的实践应用，重点介绍美国国家标准与技术研究院（National Institute of Standards and Technology,NIST）推荐的FF1算法，该算法可以达到128bit AES的安全强度。

值得注意的是即便采用FPE数据脱敏方案后数据依然可能处于我们前面两篇文章[1][2]描述的隐私泄露危险之下，特别是大数据高维关联带来的隐私泄露，因此不能简单的把数据脱敏等价成隐私保护。

2.数据脱敏

数据脱敏，是指对数据中包含的秘密或隐私信息（如个人身份识别信息、商业机密数据等）进行数据变形处理，使得恶意攻击者无法从经过脱敏处理的数据中直接获取敏感信息，从而实现对机密及隐私的防护。在金融、医疗、电信、电力等诸多行业，数据脱敏都有着非常广泛的应用。用户隐私或敏感数据泄露会对企业、用户或客户的利益和权益造成严重损害，也有可能引发严重的社会问题。

一般而言在大数据分析过程中，如果数据涉及用户隐私或商业机密的，在不违反系统规则条件下，需要对原始数据进行脱敏处理后才能提供开发测试使用，如身份证号、手机号、银行卡号、客户号等敏感数据都需要进行脱敏保护。

关于数据脱敏的算法有很多种，常见的处理方法有如下几种：

表1：常见的数据脱敏算法

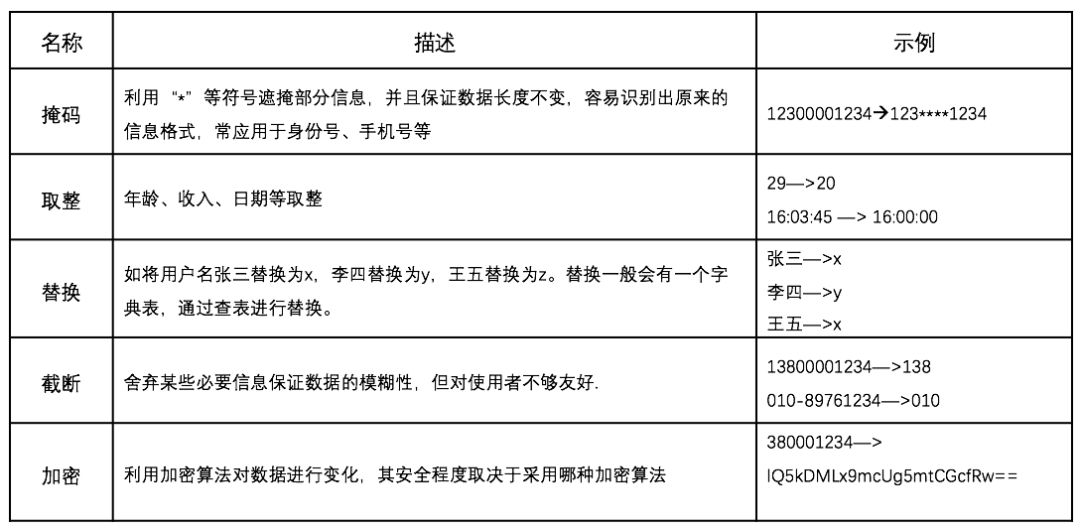
在实际业务中应用数据脱敏技术，除了数据脱敏算法以外，还需要关注数据脱敏方式。根据数据脱敏方式不同，可分为静态数据脱敏（SDM，Static Data Masking）和动态数据脱敏（DDM，Dynamic Data Masking）[4]，两者主要区别是：

静态数据脱敏（SDM），是数据存储时脱敏，存储的是脱敏数据。一般用在非生产环境，如开发、测试、外包和数据分析等环境。

动态数据脱敏（DDM），在数据使用时脱敏，存储的是明文数据。一般用在生产环境，动态脱敏可以实现不同用户拥有不同的脱敏策略。

3.脱敏实施

为了更好地保护用户隐私，需要实施细粒度的访问控制策略和最小范围的授权策略，如对数据库启用基于列（或字段）的权限控制策略。但对于用户隐私保护而言仅仅实施了细粒度权限控制是不够的，还需要配合相关的数据脱敏策略，才能更好地保护用户隐私。例如员工申请了手机号码这个字段的明文数据访问权限，就可以在授权范围内查询所有用户的手机号码，我们无法对其后续行为进行有效约束，这样就可能导致敏感信息泄露。如果启用了数据脱敏策略，员工看到的是脱敏后的数据，很难还原出原始数据。

从实践经验来看，能实施数据脱敏的场景建议一定要启用数据脱敏。数据脱敏对于企业隐私数据保护来说非常重要，但是数据脱敏有可能影响其已有业务流程和员工使用习惯，因此如何有效推动企业实施数据脱敏呢？我们可以从数据流程和数据访问制度等方面加以引导。为了更加有效地管理数据资产，可以对资产敏感程度和访问密级进行划分，例如可以把数据密级划分为5个等级，分别是L1（公开）、L2（保密）、L3（机密）、L4（绝密）和L5（私密）。对于手机号码、身份证号等敏感数据属于为L5级别，如果用户申请L5级别的明文数据需要经过一个复杂的审批流程，申请周期长，审批难度非常大。如果员工申请脱敏数据，可以将数据密级适当降低，这样审批流程可以简化，申请周期会缩短，申请成功率也会提升。对于员工而言如果脱敏是可以满足业务需求，就会优先申请脱敏数据，这样也可以促使数据脱敏技术大范围地推广应用。

表2：数据脱敏降级示例

4.格式保留加密

格式保留加密（FPE，Format Preserving Encryption，也被称之为保形加密）[3]是一类特殊对称加密算法，它可以保证加密后的密文格式与加密前的明文格式完全相同，例如通过FPE算法对由16位数字组成的银行卡号进行加密后仍为16位数字。格式保留加密常用于数据脱敏项目中，由于其可以保持加密后的数据格式不变，从而具有无需更改数据库范式以及对上层应用透明的优势。如下图所示：

表3：FPE和AES对比

FPE算法可以保证加密前后数据格式保持不变，除此之外还包括以下特点:

数据长度不变。加密前长度是N，加密后长度仍然是N
数据类型不变，加密前是数字类型，加密后仍然是数字类型。
加密过程可逆，加密后的数据可以通过密钥解密还原原始数据。

学术界关于格式保留加密的研究已经持续多年，2002年,Black 和Rogaway[5]提出了3种FPE构建方法：Prefix, Cycle-Walking和Generalized-Feistel。这3种方法成为构造FPE模型的基本方法。Generalized-Feistel方法[5]的适用性更为广泛，其核心思路是基于Feistel网络[6]来构建符合整数集大小的分组密码，并结合Cycle-Walking方法使最终密文输出在合理范围内。Feistel网络可以通过定义分组大小、密钥长度、轮次数、子密钥生成、轮函数等来构造一个分组密码，其主要流程如下图所示：

图1：Feistel网络

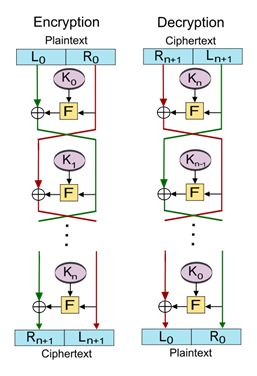
其加密算法逻辑如下：

令F为轮函数；令K1，K2，……，Kn 分别为第1，2，……，n 轮的子密钥。那么Feistel加密过程如下：

（1）将明文信息均分为两块：（L0,R0）；

（2）在每一轮中，进行如下运算（i为当前轮数）：

L_i+1= Ri；

R_i+1= Li ⊕ F（Ri,Ki）。（其中⊕为异或操作）

所得的结果即为：(R_i+1，L_i+1)。

其解密算法逻辑如下：

对于密文（R_n+1,L_n+1），我们将i由n 向0 进行，即i=n，n-1，……，0。然后对密文进行加密的逆向操作，如下：

（1）Ri = L_i+1；

（2）Li = R_i+1⊕ F（Li+1,Ki）。（其中⊕为异或操作）

所得结果为（L0,R0），即原来的明文信息。

5.FF1算法

为了进一步规范FPE的实施，美国国家标准与技术研究院（National Institute ofStandards and Technology,NIST）针对FPE发布了标准草案SP800-38G[7]，并给出了3种具体的加密算法：FF1、FF2及FF3。这些算法的主体流程是类似的，其核心均为Feistel网络结构。其中FF1和FF3都是在128bit AES算法基础上实现的线性变化，而FF2被设计出来的时候不满足期望的128bit的安全强度被弃用。FF1和FF3不同是，FF1基于经过10轮迭代，而FF3经过8轮迭代。FF3的性能略胜于FF1，但FF1的安全强度更高。因此从安全角度出发推荐利用FF1算法来实现FPE。

本文重点介绍FF1算法的使用方法和应用场景，关于该算法的安全证明和实现细节可以参阅NISTSP800-38G[7]。另外可以在Github上找到FF1的开源实现，例如Java版本的[8]、Golang版本[9]等；

实现FF1算法之前需要先了解该算法的一些基本概念和定义：

Alphabet：有限字母的字典表，并规定了输出密文的范围，例如对于手机号码而言，是十进制纯数字格式的，其Alphabet包括字符'0'-'9'。对于MAC地址而言，是十六进制数字格式，其Alphabet应该包括大写英文字母的'A'-'E'和数字'0'-'9'在内的十六个字母。

Character：Alphabet中的每一个字母称之为Character。

Radix：Alphabet中字母的个数总和，或者说Alphabet数组的长度。对于仅包含26个小写英文字母的Alphabet而言，其Radix=26。

Key：加密密钥，由于FF1是一种对称加密算法，其加密密钥和解密密钥都是相同的。FF1算法中Key长度必须是16bit、24bit和32bit三种中的一种。

Tweak：对于FF1算法来说Tweak是一个重要的概念，相当于第二密钥，可以和Key相互配合完成加密操作。例如，将FF1算法应用在手机号码FPE加密中的话，如果我们仅仅加密中间4位，前3位和后4位保持不变。中间4位数字会产生1万种可能。对于有着1百万条手机号码记录来说，大概每100张会有相同的中间4位数字，也就是对于不同的明文FPE加密结果是相同。这种情况下，我们可以把手机号码的前3位和后4位作为tweak，然后再把中间4位加密，那么其结果相同的概率就会大大降低。

FF1算法使用流程如下：

1.设计Alphabet字典表。例如手机号、银行卡号等字段可以采用数字字母字典表（'0'-'9'），对于英文姓名等采用英文字母字典表（小写字母'a'-'z'、大写字母'A'-'Z'），对于Mac地址、IMEI等可以采用十六进制数字字母字典表（'0'-'9'和'A'-'E'）；

2.设计Tweak取值。Tweak是为了解决因局部加密而导致结果冲突问题，通常情况下将数据的不可变部分作为Tweak。例如对手机号码FPE而言，可以将手机号码的前3位和后4位联合起来当做Tweak，将把中间4位通过FPE加密。

3.设计Key。对于FPE而言Key的长度必须是16bit、24bit和32bit三种中的一种。另外Key是一个秘密需要妥善保存。在不需要解密的情况下key可以随机选择，这样可以获取更高的安全性。

4.构造FPE算法对数据进行加密和解密操作。

6.总结

由于FPE保持密文和明文具有相同格式的特征，因此特别适用于数据脱敏领域。一方面FPE是一种加密方式，可以对敏感数据（例如手机号码、身份证号码、银行卡号等）进行加密存储，可以有效降低因黑客入侵导致的敏感信息泄露。另一方面基于FPE实现数据脱敏在一定程度上可以替换传统基于掩码的数据遮蔽方案，并对敏感数据进行伪装转换使得加密后的数据看起来和真实数据一模一样，在测试、开发、外包等环境中使用更加友好。在使用FPE进行数据脱敏的时候如果不考虑解密，可以为FPE生成随机密钥，这样安全性会更好。但如果需要解密操作就需要额外设计一套FPE密钥存储管理机制，以防止密钥被窃取。

基于FPE的数据脱敏方案是隐私保护的重要手段之一，然而仅仅依靠数据脱敏并不能解决所有隐私保护问题，即便采用FPE数据脱敏方案后数据依然可能处于我们前面两篇文章[1][2]描述的隐私泄露危险之下，特别是在了解相关数据背景知识的前提下运行大数据高维关联分析，脱敏后隐私数据可能被再次复原出来，因此不能简单的将数据脱敏等价成隐私保护。